Artuš, Bambi, Celestia a Dolores sa hádajú o tom, kto z nich ich prihlásil na súťaž. Po otázke, kto to urobil, nám povedia toto:

• Artuš: “Bambi poslala prihlášku. Ja som to nebol.”
• Bambi: “Celestia ju poslala. Artuš to naozaj nebol.”
• Celestia: “Bambi to nebola. Ja som poslala tú prihlášku.”
• Dolores: “Celestia to nebola. Bol to Artuš.”

Medzi Artušom a Bambi prebehol tento rozhovor:

• Bambi: "Koľko z tvojich súrodencov má práve $3$ sestry?"
• Artuš: "Aspoň polovica z nich."
• Bambi: "A koľko z tvojich súrodencov má aspoň $4$ bratov?"
• Artuš: "Nie viac ako polovica z nich."

Číslo letu je trojciferné prirodzené číslo, ktoré má všetky svoje cifry nepárne. Ak k nemu pripočítam $421$, dostanem trojciferné číslo, ktoré má všetky svoje cifry párne. Nájdite všetky čísla letu, ktoré to spĺňajú.

Máme úsečku $AD$. Na nej vyznačíme body $B$ a $C$ tak, že $|AB| < |AC|$ a platí $|AC| = 2 \cdot |AB| + |CD|$. Vieme, že $CXB$ je pravouhlý trojuholník s pravým uhlom pri vrchole $C$ a $45^{\circ}$ veľkým vnútorným uhlom pri $X$. Jeho strana $CX$ je dlhá $14$ cm. Aká je dlhá pôvodná úsečka $AD$?

Mýtický boh Šari ukladá hory do políčok mriežky $3\times3$. Do každého políčka môže položiť ľubovoľný počet hôr a niektoré políčka môže nechať aj prázdne. Keď ich uloží, tak spočíta počet hôr v každom riadku aj v každom stĺpci. Snaží sa ich uložiť tak, aby týchto $6$ počtov bolo navzájom rôznych. Koľko najmenej hôr na to mýtický boh Šari potrebuje? Vysvetlite, prečo mu na to menej hôr nestačí a nakreslite, ako ich má uložiť.

Ujo mal kalkulačku, ktorá vybuchne, ak sa na nej zobrazí číslo menšie ako $0$. Na začiatku je na kalkulačke číslo $1$. Sú na nej iba tlačítka s operáciami $-6, -42$ a $*7$. Koľko čísel od $1$ do $1000$ (vrátane) vie pomocou týchto operácií na kalkulačke získať? Na kalkulačke sa počas výpočtu môžu zobraziť aj čísla väčšie ako $1000$.

Dolores má presýpacie hodiny, ktoré sa celé presypú za $4$ minúty, a presýpacie hodiny, ktoré sa presypú za $11$ minút. Navrhnite postup, ako pomocou týchto dvoch presýpacích hodín odmerá $10$ minút.

Celestia si predstavovala päť kamarátov, ktorí sa dohadujú, kto spolu pôjde na dovolenku. Zistite, kto nakoniec šiel, ak viete, že platí:

• Ak išla Uršula, tak išiel aj Zdeno. (To znamená, že Zdeno môže ísť, aj keď Uršula nepôjde.)
• Išla buď Xilofénia, alebo Viktor, alebo obaja spolu.
• Išiel buď Zdeno, alebo Yvon, ale nie obaja spolu.
• Viktor a Yvon išli buď obaja spolu, alebo ani jeden.
• Ak išla Xilofénia, tak išli aj Uršula a Viktor. (Každý z dvojice Uršula a Viktor môže ísť, aj keď Xilofénia nepôjde.)

Gazdiná Iréna pripravila $25$ sushi pre ľudí pri stole. Potom spočítala, že by si každý mohol zobrať dva, ale po troch by už na všetkých nevyšlo. Povedala si, že keby vyrobila ešte $10$ sushi, mohol by si každý pri stole vziať tri, ale štyri nie každý. Nakoniec prichystala dokopy $52$ sushi. Každý pri stole by si teda mohol vziať štyri sushi, ale po päť by už na všetkých nevyšlo. Koľko ľudí pri stole gazdiná Iréna čakala?

Do šachovnice $7\times7$ vpíšeme postupne čísla od $1$ do $49$ tak, že začneme v ľavom hornom rohu, a pokračujeme postupne po riadkoch. Vieme na túto šachovnicu položiť $3$ tetrominá ako na obrázku tak, aby súčet všetkých čísel prekrytých týmito tetrominami (tetrominá sa nemôžu prekrývať navzájom) bol deliteľný $4$?

Čierni nindžovia sa chystajú útočiť a starček predpovedal, za koľko minút by prišli. Predpovedal $5$ časov v minútach (minúty sú celé a hodnoty predpovedí sa môžu opakovať). Vypočítal súčty všetkých dvojíc medzi nimi. Vyšli mu však len tri rôzne výsledky: $57, 70$ a $83$. Aký bol najväčší počet minút, ktorý predpovedal?

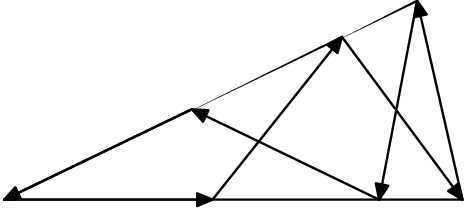
E skáče svojím prstom po dvoch ramenách uhla ako na obrázku. Všetky jeho skoky sú rovnakej dĺžky. Začína z vrcholu uhla a po siedmich skokoch sa vráti naspäť do tohto vrcholu. Aká je veľkosť tohto uhla?