
Pozrite sa na
Správa účtu
Podporili nás

Zadania seminára Malynar, 31. ročník - Zimný smester
Vzorové riešenia 1. série nájdeš v časopise Malynar-31-2
Vzorové riešenia 2. série nájdeš v časopise Malynar-31-3
Prosíme všetkých riešiteľov, aby dbali na čitateľnosť nahratých riešení - namiesto odfotenia riešenia zo zošita riešenie radšej napíšte na čistý papier formátu A4, oskenujte (prípadne využite mobilné aplikácie, ktoré skener nahradia) a nahrajte ho správne orientované vo formáte PDF. Riešiteľ riskuje stratu bodov za všetko, čo opravovatelia neprečítajú.
Ak nevieš pohnúť ďalej s niektorou z úloh, skús sa pozrieť na pár tipov.
Termín série: 25. október 2021 20:00:00
1. Lysander si pamätá, že jeho kód je štvorciferné číslo, pre ktoré platí, že súčet prvej a tretej cifry je rovnaký ako súčet druhej a štvrtej cifry, a zároveň súčet prvej a druhej cifry je rovnaký ako súčet tretej a štvrtej cifry. Číslo je deliteľné piatimi a má ciferný súčet $18$. Aké rôzne kódy mohol Lysander mať?
2. V meste, kde žije Lysander, sa ľudia delia na dve skupiny podľa kapiel, ktoré počúvajú: Mesačné ropuchy a Ružoví skokani. Fanúšikovia Mesačných ropúch vždy hovoria pravdu a fanúšikovia Ružových skokanov vždy klamú. Lysander si z rozhovoru pri vedľajšom stole vypočul tieto výroky:
- Artemis: „Teo je fanúšik inej skupiny ako ja.“
- Apollo: „Luna je fanúšik Ružových skokanov.“
- Luna: „Apollo je fanúšik Ružových skokanov.“
- Teo: „Medzi nami štyroma sú aspoň dvaja fanúšikovia Mesačných ropúch.“
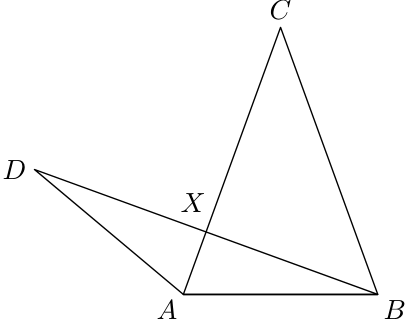
3. Na pláne výstavby je rovnoramenný trojuholník $ABC$ so základňou $AB$ a s uhlom $40$ stupňov pri vrchole $C$ a aj rovnoramenný trojuholník $ABD$ so základňou $BD$ tak, že $AC$ je os uhla $BAD$. Označme $X$ priesečník úsečiek $AC$ a $BD$. Určte veľkosť uhla $CXD$.

4. Predavač si predstavil trojciferné číslo a jeho zákazníci sa ho pokúsili uhádnuť. Toto sú ich pokusy:
- zákazník: $218$,
- zákazník: $571$,
- zákazník: $732$,
- zákazník: $853$.
5. Dvaja hráči hrajú naháňačku na šachovnici $8\times 8$. Začínajú v protiľahlých rohoch a striedajú sa v ťahoch. Prvý hráč vyhrá, ak doženie druhého, teda ak stúpi na to isté políčko ako on. Ťahať môžu iba o jedno políčko v hociktorom zo štyroch smerov, ktoré s pôvodným políčkom susedia stranou. Prvý hráč začína. Doženie niekedy prvý hráč druhého? Ak áno, na koľko najmenej ťahov? Ak nie, prečo?
6. Vlak má $5$ vozňov a v každom z nich je niekoľko cestujúcich (všade aspoň $1$). Dvaja cestujúci sú susedia, ak sedia v rovnakom alebo vo vedľajších vozňoch. Každý cestujúci má buď práve $50$, alebo práve $100$ susedov. Koľko cestujúcich môže byť vo vlaku? Nájdite všetky možnosti.
Vzorové riešenia 1. série nájdeš v časopise Malynar-31-2
Vzorové riešenia 2. série nájdeš v časopise Malynar-31-3
Prosíme všetkých riešiteľov, aby dbali na čitateľnosť nahratých riešení - namiesto odfotenia riešenia zo zošita riešenie radšej napíšte na čistý papier formátu A4, oskenujte (prípadne využite mobilné aplikácie, ktoré skener nahradia) a nahrajte ho správne orientované vo formáte PDF. Riešiteľ riskuje stratu bodov za všetko, čo opravovatelia neprečítajú.
Ak nevieš pohnúť ďalej s niektorou z úloh, skús sa pozrieť na pár tipov.
Termín série: 29. november 2021 20:00:00
1. Na mape boli vyznačené $4$ mestá na jednej priamke a vzdialenosť medzi každou dvojicou miest. Mapa ale bola stará, na jednej vzdialenosti bol fľak a číslo pod ním nebolo možné prečítať. Zvyšné vzdialenosti boli: $2$, $3$, $11$, $12$ a $14$. Tá, ktorú nebolo vidno kvôli fľaku, bola tretia najkratšia. Aká bola táto vzdialenosť?
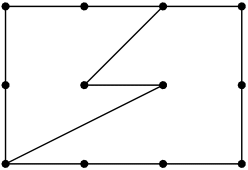
2. Na obrázku je znázornená deka, ktorú plietol Apollo z dvoch častí, päťuholníka a šesťuholníka v bodoch mriežky štvorcovej siete. Určite obsah šesťuholníka, ak päťuholník má obsah $15$.

3. V malej dedinke žije $5$ pravdovravcov a $1$ klamár. Môžeme si dvakrát vybrať ktorúkoľvek dvojicu a jednému z tejto dvojice položiť otázku, či je ten druhý klamár. Chceme s istotou určiť $4$ pravdovravcov. Akým spôsobom sa máme pýtať?
4. Z čísla $9876543210$ vyškrtni čo najmenší počet cifier tak, aby cifra na mieste desiatok bola trikrát menšia ako cifra na mieste tisícok a cifra na mieste jednotiek bola o tri menšia ako cifra na mieste stoviek. Nájdi všetky riešenia.
5. Každému zo svojich piatich spolubývajúcich chce Lysander darovať niekoľko palaciniek, každému aspoň jednu. Spolubývajúci vyslovili nasledujúce priania:
- Alfred: Chcem dostať rovnako veľa palaciniek ako Boris.
- Boris: Chcem dostať viac palaciniek ako Cyril.
- Cyril: Nechcem dostať rovnako veľa palaciniek ako Daniel.
- Daniel: Chcem dostať nepárny počet palaciniek.
- Emil: Chcem mať iný počet palaciniek ako ktokoľvek iný.
6. Artemis a Vincent majú na stole kôpku $100$ kamienkov a hrajú takúto hru: hráč vo svojom ťahu vezme vždy z kôpky nejaký počet kamienkov, ktorý je deliteľom aktuálneho počtu kamienkov v kôpke, nesmie však vziať všetky kamienky. V ťahoch sa striedajú a Artemis začína. Hráč, po ktorého ťahu zostane $1$ kamienok na kôpke, vyhráva. Určte, ktorý z hráčov má víťaznú stratégiu a ako vyzerá.
Newsletter
Nenechajte si ujsť akcie, ktoré chystáme a odoberajte náš newsletter!

 Prosím čakajte ...
Prosím čakajte ...